Archive for the ‘TAPENADE’ Category

Using TAPENADE

November 27, 2009

TAPENADE is a Automatic Differentiation (AD) tool for FORTRAN. It generates differentiation code by source code transformation. This post gives examples of TAPENADE usage.

TAPENADE Example

For illustration of TAPENADE usage, following test expression is selected

\displaystyle z\left(x,y\right)=\sin \left( x+2y\right) \cos \left( x-\sin \left( y\right) \right)

This expression/function is coded in FORTRAN as a subroutine which takes 3 arguments whose in/out behaviour is stated by intent directives

  • x,y : input arguments
  • z : output arguments
    • ! FILE : test1.f90
subroutine test1(x,y,z)
	real, intent(in) :: x,y
	real, intent(out) :: z

	z = sin(x+2*y)*cos(x-sin(y));
end subroutine test1

    TAPENADE executed to differentiate test1 subroutine (in tangent mode) generates following differentiation code

    !        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of test1 in forward (tangent) mode:
!   variations  of output variables: z
!   with respect to input variables: x y
SUBROUTINE TEST1_D(x, xd, y, yd, z, zd)
  IMPLICIT NONE
  REAL, INTENT(IN) :: x, y
  REAL, INTENT(IN) :: xd, yd
  REAL, INTENT(OUT) :: z
  REAL, INTENT(OUT) :: zd
  REAL :: arg1
  REAL :: arg1d
  INTRINSIC COS
  INTRINSIC SIN
  arg1d = xd - yd*COS(y)
  arg1 = x - SIN(y)
  zd = (xd+2*yd)*COS(x+2*y)*COS(arg1) - SIN(x+2*y)*arg1d*SIN(arg1)
  z = SIN(x+2*y)*COS(arg1)
END SUBROUTINE TEST1_D

    Note that each input and output variable that user specified caused insertion of “differentials” of those variables, that is, the input code

    subroutine test1(x,y,z)

    results in

    SUBROUTINE TEST1_D(x, xd, y, yd, z, zd)

    In this example,

  • differentials dx,dy for input arguments x,y
  • differential dz for output argument z

    • are inserted just after the original argument.

    Actual differential of test1 function is (total differential)

    \displaystyle dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy

    with

    \frac{\partial z}{\partial x}=\cos \left( x+2y\right) \cos \left( x-\sin \left( y\right) \right) -\sin \left( x+2y\right) \sin \left( x-\sin \left( y\right) \right)
    \frac{\partial z}{\partial y}=2\cos \left( x+2y\right) \cos \left( x-\sin \left( y\right) \right) +\sin \left( x+2y\right) \sin \left( x-\sin \left( y\right) \right) \cos \left( y\right)

    Note that in order to compute partial derivatives \frac{\partial z}{\partial x} and \frac{\partial z}{\partial y}, the generated derivative routine test1_d must be called twice

    ! derivative computation point
x = ...
y = ...
xd = 1.0
yd = 0.0
CALL TEST1_D(x, xd, y, yd, z, zd) ! z and zd ~ dz/dx is obtained
xd = 0.0
yd = 1.0
CALL TEST1_D(x, xd, y, yd, z, zd) ! z and zd ~ dz/dy is obtained

    In order to avoid such multiple calls, TAPENADE has an alternate differentiation mode called “Tangent Vectorial Mode”

    If TAPENADE code is generated with this option then following differentiation code is obtained

    !        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of test1 in forward (tangent) mode: (multi-directional mode)
!   variations  of output variables: z
!   with respect to input variables: x y
SUBROUTINE TEST1_DV(x, xd, y, yd, z, zd, nbdirs)
  USE DIFFSIZES
!  Hint: nbdirsmax should be the maximum number of differentiation directions
  IMPLICIT NONE
  REAL, INTENT(IN) :: x, y
  REAL, INTENT(IN) :: xd(nbdirsmax), yd(nbdirsmax)
  REAL, INTENT(OUT) :: z
  REAL, INTENT(OUT) :: zd(nbdirsmax)
  REAL :: arg1
  REAL :: arg1d(nbdirsmax)
  REAL :: arg2
  REAL :: arg2d(nbdirsmax)
  INTEGER :: nd
  INTEGER :: nbdirs
  INTRINSIC COS
  INTRINSIC SIN
  arg1 = x + 2*y
  arg2 = x - SIN(y)
  DO nd=1,nbdirs
    arg1d(nd) = xd(nd) + 2*yd(nd)
    arg2d(nd) = xd(nd) - yd(nd)*COS(y)
    zd(nd) = arg1d(nd)*COS(arg1)*COS(arg2) - SIN(arg1)*arg2d(nd)*SIN(&
&      arg2)
  END DO
  z = SIN(arg1)*COS(arg2)
END SUBROUTINE TEST1_DV

    Note that generated code executes differentiation code for all given differentiation directions inside a loop. This, in effect, corresponds to calling “single-direction” mode successively, but with the direction loop inside the differentiation code, subroutine arguments are not passed to calls again and again, increasing the efficiency of code. Another benefit of this mode is hiding details of successive calls.

    Following (incomplete) program illustrates use of “multi-directional” mode.

    integer, parameter :: nbdirs = 8
real*8 xd(nbdirs),yd(nbdirs)
xd = (/1.0, 0.0/)
yd = (/0.0, 1.0/)
call TEST1_DV(x, xd, y, yd, z, zd, nbdirs) ! zd contains all partial derivatives

    TAPENADE GUI Usage

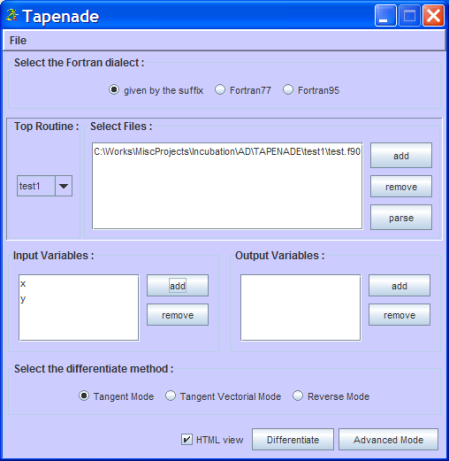
    First click add button

    Select the source fi le(s) test.f90

    In listbox component all source code added is shown

    Click Parse Button. On the left drop-down list box, subroutines/functions available in parsed source codes will appear

    In input variables, click Add and select x,y

    Pressing OK will add selected variable(s) to input variables listbox component

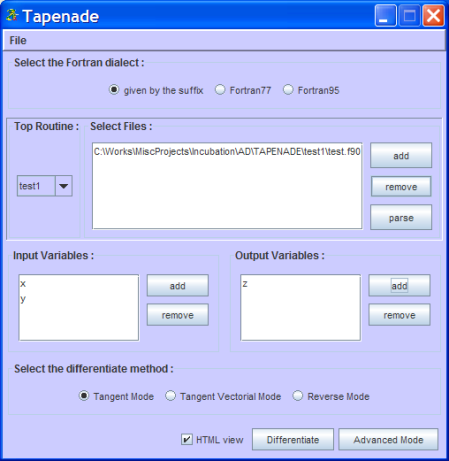
    In output variable, click Add and select z

    Pressing OK will add selected variable(s) to output variables listbox component

    Finally select differentiation mode and click differentiate. This will generate code and automatically open html report page (if browser is properly defi ned in environment)

    Reverse Mode

    Reverse mode first illustrated by a sample routine from INRIA report RR-5237 . This routine implements function

    \displaystyle o_1 = z\left( x^{2}+1\right) y^{2} if \displaystyle \left( x^{2}+1\right) y^{2} < 10
    \displaystyle o_1 = 10z otherwise

    Exact gradient of this expression is

    \displaystyle \frac{\partial o_{1}}{\partial\left( x,y,z\right) } = \left[ 2zxy^{2}, z\left( x^{2}+1\right), \left( x^{2}+1\right) y^{2}\right]

    if \displaystyle \left( x^{2}+1\right) y^{2} < 10

    subroutine sub1(x,y,z,o1)
	real, intent(in) :: x,y,z
	real, intent(out) :: o1

	x = y*x
	r = x*x+y*y   ! x**2*y**2+y**2
	if (r>10.0) then
		r = 10.0
	end if

	o1 = r*z      ! z*(x**2*y**2+y**2)
end subroutine sub1

    differentiating this routine in reverse mode using TAPENADE yields

    !        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of sub1 in reverse (adjoint) mode:
!   gradient, with respect to input variables: x y z o1
!   of linear combination of output variables: o1
SUBROUTINE SUB1_B(x, xb, y, yb, z, zb, o1, o1b)
  IMPLICIT NONE
  REAL :: x, y, z
  REAL :: xb, yb, zb
  REAL :: o1
  REAL :: o1b
  REAL :: r
  REAL :: rb
  INTEGER :: branch
  CALL PUSHREAL4(x)
  x = y*x
  r = x*x + y*y
  IF (r .GT. 10.0) THEN
    r = 10.0
    CALL PUSHINTEGER4(1)
  ELSE
    CALL PUSHINTEGER4(0)
  END IF
  rb = z*o1b
  zb = r*o1b
  CALL POPINTEGER4(branch)
  IF (.NOT.branch .LT. 1) rb = 0.0
  xb = 2*x*rb
  CALL POPREAL4(x)
  yb = x*xb + 2*y*rb
  xb = y*xb
  o1b = 0.0
END SUBROUTINE SUB1_B

    Note that TAPENADE does not include evaluation of original function in reverse-mode. Some literature states that this TAPENADE specific.

    Driver program for reverse differentiation code is given below. Program computes gradient at x=1,y=1.5,z=2 which bypass the if-statement in the code. The gradient of linear combination selected output variables o1 is returned in differentials of input variables xb,yb,zb. Weightings are specified in differentials of output variables o1b. So since in this example there is one output variable, o1b=1 yields gradient of o1 in xb,yb,zb.

    program usesub1b
	implicit none
	real x,xb,y,yb,z,zb,o1,o1b
	o1b = 1.0
	x = 1.0
	y = 1.5
	z = 2.0
	call SUB1_B(x, xb, y, yb, z, zb, o1, o1b)

	print *, "TAPENADE computed gradient:"
	write(6,'(3(F12.6))') xb,yb,zb

	print *, "exacy gradient (without if):"
	write(6,'(3(F12.6))') z*2*x*y**2, z*(x**2+1)*2*y, (x**2+1)*y**2
end program usesub1b

    Note that reverse mode differentiation code contains PUSH/POP (store value-retrieve value) operations. To my knowledge, this is the case when some branching like if-statement, subroutine-call occurs in “source” code. Again to my knowledge, number of occurrences of PUSH/POP operations is dependent on the AD tool reverse mode differentiation strategies “store-all”, “re-compute-all”,… . These PUSH/POP operations are defined on separate source files (ADFirstAidKit.tar.gz) available for download at TAPENADE site. Compilation is described in TAPENADE tutorial. For this example, only adBuffer.f,adStack.c is needed. Following the instructions in tutorial code is compiled by following commands

    rem from http://www-sop.inria.fr/tropics/tapenade/tutorial.html
gfortran -c usesub1b.f90
gfortran -c sub1_b.f90
gfortran -c adBuffer.f
gcc -c adStack.c

gfortran sub1_b.o adBuffer.o adStack.o usesub1b.o -o usesub1b

    output of executable is as follows

     TAPENADE computed gradient:
    9.000000   12.000000    4.500000
 exacy gradient (without if):
    9.000000   12.000000    4.500000

    Second example is given to illustrate concept of gradient of linear combination of output variables. In this example two input variables map to \left(x,y\right) \rightarrow \left(\begin{array}[c]{c}o_{1}\\o_{2}\end{array}\right) =\left( \begin{array} [c]{c} \frac{x^{2}-y^{2}}{2}\\ \frac{x^{2}+y^{2}}{2} \end{array}\right) . This function code is given below

    subroutine samplefun(x,y,z1,z2)
	real, intent(in) :: x,y
	real, intent(out) :: z1,z2

	z1 = 0.5*(x**2-y**2)
	z2 = 0.5*(x**2+y**2)

end subroutine samplefun

    and its reverse-mode differentiation is obtained as

    !        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of samplefun in reverse (adjoint) mode:
!   gradient, with respect to input variables: x y z1 z2
!   of linear combination of output variables: z1 z2
SUBROUTINE SAMPLEFUN_B(x, xb, y, yb, z1, z1b, z2, z2b)
  IMPLICIT NONE
  REAL, INTENT(IN) :: x, y
  REAL :: xb, yb
  REAL :: z1, z2
  REAL :: z1b, z2b
  xb = 0.5*2*x*z1b + 0.5*2*x*z2b
  yb = 0.5*2*y*z2b - 0.5*2*y*z1b
  z1b = 0.0
  z2b = 0.0
END SUBROUTINE SAMPLEFUN_B

    Define linear combination of two outputs o_1,o_2 as J=w_{1}o_{1}+w_{2}o_{2}=w_{1}\frac{x^{2}-y^{2}}{2}+w_{2}\frac{x^{2}+y^{2}}{2} then gradient of this new quantity is

    \nabla J=\left[ \begin{array} [c]{c} \left( w_{1}+w_{2}\right) x\\ \left( w_{2}-w_{1}\right) y \end{array} \right]

    To check this in differentiation code, manually call SAMPLEFUN_B with z1b=w1, z2b=w2 to get

    xb = 0.5*2*x*z1b + 0.5*2*x*z2b => 0.5*2*x*w1 + 0.5*2*x*w2 \rightarrow x w_1+x w_2
    yb = 0.5*2*y*z2b - 0.5*2*y*z1b => 0.5*2*y*z2b - 0.5*2*y*z1b \rightarrow y w_2-y w_1

    which is recognized as actual gradient as required.

    Missing functions

    TAPENADE handles all common mathematical functions sin, cos, exp, sqrt in the differentiation process, but if some function is not known to TAPENADE and/or its implementation is missing, instead of giving an error and quitting, TAPENADE continues with generation of differentiation code using the apparent signature of the function. Then user is responsible for supplying differentiation code of the function with missing implementation. To exemplify situation, the function

    \displaystyle s\left(\boldsymbol{r}\right)=\frac{\sin\left(\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}\right)}{\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}}

    that computes the sinc-of-radial distance in nD space (using the DOT_PRODUCT) is differentiated with TAPENADE. Code to be differentiated is given below

    ! FILE:radsinc.f90
subroutine radsinc(r,n,rs)
	integer, intent(in) :: n
	real, intent(in) :: r(n)
	real, intent(out) :: rs

	real rad

	rad = sqrt(dot_product(r,r))
	if (rad==0) then
		rs = 1.0
	else
		rs = sin( rad ) / rad
	end if
end subroutine radsinc

    and differentiation code in tangent mode is obtained as

    ! FILE: radsinc_d.f90
!        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of radsinc in forward (tangent) mode:
!   variations  of output variables: r rs
!   with respect to input variables: r
SUBROUTINE RADSINC_D(r, rd, n, rs, rsd)
  IMPLICIT NONE
  INTEGER, INTENT(IN) :: n
  REAL, INTENT(IN) :: r(n)
  REAL, INTENT(IN) :: rd(n)
  REAL, INTENT(OUT) :: rs
  REAL, INTENT(OUT) :: rsd
  REAL :: rad
  REAL :: radd
  EXTERNAL DOT_PRODUCT
  EXTERNAL DOT_PRODUCT_D
  REAL :: DOT_PRODUCT
  REAL :: DOT_PRODUCT_D
  REAL :: result1
  REAL :: result1d
  INTRINSIC SIN
  INTRINSIC SQRT
  result1d = DOT_PRODUCT_D(r, rd, r, rd, result1)
  IF (result1 .EQ. 0.0) THEN
    radd = 0.0
  ELSE
    radd = result1d/(2.0*SQRT(result1))
  END IF
  rad = SQRT(result1)
  IF (rad .EQ. 0) THEN
    rs = 1.0
    rsd = 0.0
  ELSE
    rsd = (radd*COS(rad)*rad-SIN(rad)*radd)/rad**2
    rs = SIN(rad)/rad
  END IF
END SUBROUTINE RADSINC_D

    Actual differential of the function is

    \displaystyle ds =\frac{\boldsymbol{r}\cdot\boldsymbol{dr}}{\left(\boldsymbol{r}\cdot\boldsymbol{r}\right)^{\frac{3}{2}}}\left(\cos\left(\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}\right)\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}-\sin\left(\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}\right)\right)

    Since the function DOT_PRODUCT is not in TAPENADE standard function list and no implementation is available, TAPENADE cannot generate a differentiation code for function DOT_PRODUCT. So it just emits the differential code result1d = DOT_PRODUCT_D(r, rd, r, rd, result1) (line 25) and expects the user to supply this function at compile time. For this reason, it informs the compiler that actual object code is defined elsewhere by inserting EXTERNAL declaration(s) in the source code (line 18). Derivative of dot product can be obtained from

    \displaystyle \frac{d}{dt}\left(\boldsymbol{a\cdot b}\right)=\frac{d\boldsymbol{a}}{dt}\cdot\boldsymbol{b}+\boldsymbol{a}\cdot\frac{d\boldsymbol{b}}{dt}

    which is translated to code as follows

    ! FILE: DOT_PRODUCT_D.f90
real function dot_product_d(a, ad, b, bd)
	implicit none
	real, intent(in), dimension(:) :: a, b, ad, bd
	dot_product_d = dot_product(ad,b) + dot_product(a,bd)
end function dot_product_d

    From the generated code, it is observed that TAPENADE generated code computes function and its derivative in the same routine, so if conformance to originally generated code is sought then above definition is updated as

    ! FILE: DOT_PRODUCT_D.f90
real function dot_product_d(a, ad, b, bd,dotprod)
	implicit none
	real, intent(in), dimension(:) :: a, b, ad, bd
	real, intent(out) :: dotprod
	dotprod = dot_product(a,b)
	dot_product_d = dot_product(ad,b) + dot_product(a,bd)
end function dot_product_d

    To test the TAPENADE generated routine following test program is used

    ! FILE: main.f90
program main
	implicit none

	interface
		real function dot_product_d(a, ad, b, bd,dotprod)
			implicit none
			real, intent(in), dimension(:) :: a, b, ad, bd
			real, intent(out) :: dotprod
		end function dot_product_d
	end interface

	real, dimension(4) :: r, rd
	real :: rs, rsd, rstrue, rsdtrue, rdotr, rdotrd, rdotr2
	real ::  dotprod,dotprod_d

	r = (/ 1., 2., 3., 4. /)		! vector in 4D
	rd = (/ 40, 30, 20, 10 /)	! rate(/differential) of vector

	! check dot product
	rdotr = dot_product(r,r)
	rdotrd = dot_product(r,rd)
	print *, "r-dot-dr:", rdotrd
	print *, "r-dot-r :", rdotr

	! check derivative of dot product
	dotprod_d = dot_product_d(r, rd, r, rd, rdotr2)
	print *, "r-dot-r   :", rdotr2
	print *, "d(r-dot-r):", dotprod_d

	! call TAPENADE generated routine
	! SUBROUTINE RADSINC_D(r, rd, n, rs, rsd)
	call RADSINC_D(r, rd, 4, rs, rsd)

	! compute analytical result
	rsdtrue = (rdotrd/rdotr**1.5)*(cos(sqrt(rdotr))*sqrt(rdotr)-sin(sqrt(rdotr)))
	rstrue = sin(sqrt(rdotr))/sqrt(rdotr)

	print *, "analytical results:"
	write (*,'(A8,F16.8,X,A8,F16.8)')  "sinc = ",rstrue, "dsinc = ",rsdtrue

	print *, "TAPENADE results:"
	write (*,'(A8,F16.8,X,A8,F16.8)')  "sinc = ",rs, "dsinc = ",rsd
end program main

    Compilation command is

    gfortran dotproduct_d.f90 radsinc_d.f90 main.f90 -o main.exe

    Program tests the routine for the inputs

    r=\left[1,2,3,4\right]\\dr=\left[40,30,20,10\right]

    output of program is given below

     r-dot-dr:   200.00000
 r-dot-r :   30.000000
 r-dot-r   :   30.000000
 d(r-dot-r):   400.00000
 analytical results:
 sinc =      -0.13172643 dsinc =       5.49430418
 TAPENADE results:
 sinc =      -0.13172643 dsinc =       5.49430418

    showing that the results agree

    Note that main program contains an interface declaration for dot_product_d. This is required for routines with assumed shaped array arguments as explained in Fortran Bugs/Surprises. Since TAPENADE generated routine also uses the routine dot_product_d same interface is added to SUBROUTINE RADSINC_D .This eliminates some of the previous declarations added by TAPENADE. Modified version of TAPENADE code is given below

    ! FILE: RAD_SINC.f90
!        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of radsinc in forward (tangent) mode:
!   variations  of output variables: r rs
!   with respect to input variables: r
SUBROUTINE RADSINC_D(r, rd, n, rs, rsd)
  IMPLICIT NONE
  INTEGER, INTENT(IN) :: n
  REAL, INTENT(IN) :: r(n)
  REAL, INTENT(IN) :: rd(n)
  REAL, INTENT(OUT) :: rs
  REAL, INTENT(OUT) :: rsd
  REAL :: rad
  REAL :: radd

  interface
  	real function dot_product_d(a, ad, b, bd,dotprod)
  		implicit none
  		real, intent(in), dimension(:) :: a, b, ad, bd
  		real, intent(out) :: dotprod
		end function dot_product_d
	end interface

! Following declaration no more needed due to above interface definition
!EXTERNAL DOT_PRODUCT
!EXTERNAL DOT_PRODUCT_D
!REAL :: DOT_PRODUCT
!REAL :: DOT_PRODUCT_D

  REAL :: result1
  REAL :: result1d
  INTRINSIC SIN
  INTRINSIC SQRT
  result1d = DOT_PRODUCT_D(r, rd, r, rd, result1)
  IF (result1 .EQ. 0.0) THEN
    radd = 0.0
  ELSE
    radd = result1d/(2.0*SQRT(result1))
  END IF
  rad = SQRT(result1)
  IF (rad .EQ. 0) THEN
    rs = 1.0
    rsd = 0.0
  ELSE
    rsd = (radd*COS(rad)*rad-SIN(rad)*radd)/rad**2
    rs = SIN(rad)/rad
  END IF
END SUBROUTINE RADSINC_D

    Lines 18-24 are the modifications to original code and 27-30 are the commented lines.

    Similar Technique

    For some cases, need for derivative of missing function may be avoided by some minor modifications to source code. For example suppose that there is a routine that assembles a linear system (a matrix and a RHS vector) and solves linear system using a subroutine from compiled library whose source code is not available

    subroutine SOLVE(input1, input2, x, n)
	integer, intent(in) :: n
	real, intent(in) :: input1, input2
	real, intent(out) :: x(n)

	real :: A(n,n), b(n)

	call assemble(input1, input2, A, b, n)
	call solveLinearSystem(A,b,x)
end subroutine SOLVE

    when differentiated in tangent mode, following code is obtained from TAPENADE

    !        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of solve in forward (tangent) mode:
!   variations  of output variables: x input1 input2
!   with respect to input variables: input1 input2
SUBROUTINE SOLVE_D(input1, input1d, input2, input2d, x, xd, n)
  IMPLICIT NONE
  INTEGER, INTENT(IN) :: n
  REAL, INTENT(IN) :: input1, input2
  REAL, INTENT(IN) :: input1d, input2d
  REAL, INTENT(OUT) :: x(n)
  REAL, INTENT(OUT) :: xd(n)
  REAL :: a(n, n), b(n)
  REAL :: ad(n, n), bd(n)
  EXTERNAL ASSEMBLE
  EXTERNAL ASSEMBLE_D
  EXTERNAL SOLVELINEARSYSTEM
  EXTERNAL SOLVELINEARSYSTEM_D
  ad = 0.0
  bd = 0.0
  CALL ASSEMBLE_D(input1, input1d, input2, input2d, a, ad, b, bd, n)
  xd = 0.0
  CALL SOLVELINEARSYSTEM_D(a, ad, b, bd, x, xd)
END SUBROUTINE SOLVE_D

    but as stated in beginning, there is no way to obtain or too difficult/impractical to obtain differentiation code SOLVELINEARSYSTEM_D. Trick is to obtain derivatives by some manipulation on the total differential of original expression \mathbf{Ar}=\mathbf{b} \Rightarrow d\mathbf{A}\cdot\mathbf{r}+\mathbf{A}\cdot d\mathbf{r}=d\mathbf{b} which yields

    \displaystyle d\mathbf{r}=\mathbf{A}^{-1}\cdot\left(d\mathbf{b}-d\mathbf{A}\cdot\mathbf{r}\right)

    To utilize this formula, TAPENADE code is modified as follows

    !        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of solve in forward (tangent) mode:
!   variations  of output variables: x input1 input2
!   with respect to input variables: input1 input2
SUBROUTINE SOLVE_D(input1, input1d, input2, input2d, x, xd, n)
  IMPLICIT NONE
  INTEGER, INTENT(IN) :: n
  REAL, INTENT(IN) :: input1, input2
  REAL, INTENT(IN) :: input1d, input2d
  REAL, INTENT(OUT) :: x(n)
  REAL, INTENT(OUT) :: xd(n)
  REAL :: a(n, n), b(n)
  REAL :: ad(n, n), bd(n)
  EXTERNAL ASSEMBLE
  EXTERNAL ASSEMBLE_D
  EXTERNAL SOLVELINEARSYSTEM
  EXTERNAL SOLVELINEARSYSTEM_D
  ad = 0.0
  bd = 0.0
  CALL ASSEMBLE_D(input1, input1d, input2, input2d, a, ad, b, bd, n)
  xd = 0.0
  !CALL SOLVELINEARSYSTEM_D(a, ad, b, bd, x, xd)
  CALL SOLVELINEARSYSTEM(a, b, x)
  CALL SOLVELINEARSYSTEM(a, bd-matmul(ad,x), xd)

END SUBROUTINE SOLVE_D

    Case of MATMUL function

    MATMUL function is similar to DOT_PRODUCT in that both are inner-products, essentially. Former one is acting on second and first order tensors and latter one acting on first order tensors (vectors). So similar to DOT_PRODUCT example above, manual declaration for differentiation of MATMUL would be,

    \displaystyle d\left(\mathbf{A}\cdot\mathbf{b}\right)=d\mathbf{A}\cdot\mathbf{b}+\mathbf{A}\cdot d\mathbf{b}

    which is coded as

    function matmul_d(a,ad,b,bd,ab)
	implicit none
	real, intent(in), dimension(:,:) :: a,b,ad,bd
	real, intent(out), dimension( size(a,1), size(b,2) ) :: ab

	real matmul_d( size(a,1), size(b,2) )

	ab = matmul(a,b)
	matmul_d = matmul(ad,b) + matmul(a,bd)
end function matmul_d

    Such declaration poses some Fortran 90 problems. In fortran(90) MATMUL can be used to multiply vector-matrix, matrix-matrix and matrix-vector, but above declaration gives signature for matrix-matrix version. One possible solution is to use generic-interfaces but i did not try this yet; instead i devised example consisting of only matrix-matrix multiplications. Example i choose is quadratic form given as

    \displaystyle Q = \mathbf{x}^{\top}\cdot\mathbf{A}\cdot\mathbf{x}

    whose (exact) differential is given by

    \displaystyle dQ = d\mathbf{x}^{\top}\cdot\mathbf{A}\cdot\mathbf{x}+\mathbf{x}^{\top}\cdot d\mathbf{A}\cdot\mathbf{x}+\mathbf{x}^{\top}\cdot\mathbf{A}\cdot d\mathbf{x}

    quadratic function is coded in FORTRAN as follows

    subroutine quadraticForm(A,x,QF)
	implicit none
	real, intent(in), dimension(2,2) :: A
	real, intent(in), dimension(2,1) :: x
	real, intent(out), dimension(1,1) :: QF

	real :: xp(2,1), xpt(1,2)

	xp = matmul(A,x)
	xpt = transpose(xp)
	QF = matmul(xpt,x)
end subroutine quadraticForm

    Note that vectors are replaced with column or row vector versions to conform to MATMUL_D declaration. Code obtained from tangent mode differentiation of TAPENADE is modified to yield following

    !        Generated by TAPENADE     (INRIA, Tropics team)
!  Tapenade 3.3 (r3163) - 09/25/2009 09:03
!
!  Differentiation of quadraticform in forward (tangent) mode:
!   variations  of output variables: qf x a
!   with respect to input variables: x a
SUBROUTINE QUADRATICFORM_D(a, ad, x, xd, qf, qfd)
  IMPLICIT NONE

	INTERFACE
	 	function matmul_d(a,ad,b,bd,ab)
			implicit none
			real, intent(in), dimension(:,:) :: a,b,ad,bd
			real, intent(out), dimension( size(a,1), size(b,2) ) :: ab

			real matmul_d( size(a,1), size(b,2) )
		end function matmul_d

		function dot_product_d(a,ad,b,bd,ab)
			implicit none
			real dot_product_d
			real, intent(in), dimension(:) ::  a,ad,b,bd
			real, intent(out) :: ab
		end function dot_product_d

		function transpose_d(v, vd, vt)
			implicit none
			real, dimension(:,:), intent(in) :: v, vd
			real, dimension(size(v,2), size(v,1) ), intent(out) :: vt
			real, dimension( size(v,2), size(v,1) ) :: transpose_d

		end function transpose_d

	END INTERFACE

  REAL, DIMENSION(2, 2), INTENT(IN) :: a
  REAL, DIMENSION(2, 2), INTENT(IN) :: ad
  REAL, DIMENSION(2, 1), INTENT(IN) :: x
  REAL, DIMENSION(2, 1), INTENT(IN) :: xd
  REAL, DIMENSION(1, 1), INTENT(OUT) :: qf
  REAL, DIMENSION(1, 1), INTENT(OUT) :: qfd
  REAL :: xp(2, 1), xpt(1, 2)
  REAL :: xpd(2, 1), xptd(1, 2)
  ! EXTERNAL MATMUL
  ! EXTERNAL MATMUL_D
  ! EXTERNAL TRANSPOSE
  ! EXTERNAL TRANSPOSE_D
  ! REAL :: MATMUL
  ! REAL :: MATMUL_D
  ! REAL :: TRANSPOSE
  ! REAL :: TRANSPOSE_D
  xpd = MATMUL_D(a, ad, x, xd, xp)
  xptd = TRANSPOSE_D(xp, xpd, xpt)
  qfd = MATMUL_D(xpt, xptd, x, xd, qf)
END SUBROUTINE QUADRATICFORM_D

    Test code is given below

    program main
	implicit none
	real :: A(2,2), AD(2,2), x(2), xd(2), qf, qfd

	A = reshape( (/ 1,2,2,1 /), (/2,2/) )
	AD = reshape( (/ -3,4,5,1 /), (/2,2/) )
	x = (/ 3,4 /)
	xd = (/ 7,2 /)

	call quadraticForm(A,x,QF)

	print *, A
	print *, AD
	print *, qf

	! SUBROUTINE QUADRATICFORM_D(a, ad, x, xd, qf, qfd)
	call QUADRATICFORM_D(A, AD, x, xd, qf, qfd)

	print *, qfd

end program main

    Test inputs are

    \mathbf{A}=\left[\begin{array}{cc}1 & 2\\2 & 1\end{array}\right]

    d\mathbf{A}=\left[\begin{array}{cc}-3 & 5\\4 & 1\end{array}\right]

    \mathbf{x}=\left[\begin{array}{c}3\\4\end{array}\right]

    d\mathbf{x}=\left[\begin{array}{c}7\\2\end{array}\right]

    and outputs are

     A  :    1.0000000       2.0000000       2.0000000       1.0000000
 AD :   -3.0000000       4.0000000       5.0000000       1.0000000
 QF :    73.000000
 dQF:    291.00000

    Manual calculation (not shown here) results in 291, also.

    Compilation and extra code is given below

    rem compilation of MATMUL example
gfortran main.f90  quadraticForm.f90 quadraticform_d.f90 missingfunctions.f90   -o main.exe

    ! FILE: MissingFunctions.f90
function matmul_d(a,ad,b,bd,ab)
	implicit none
	real, intent(in), dimension(:,:) :: a,b,ad,bd
	real, intent(out), dimension( size(a,1), size(b,2) ) :: ab

	real matmul_d( size(a,1), size(b,2) )

	ab = matmul(a,b)
	matmul_d = matmul(ad,b) + matmul(a,bd)
end function matmul_d

real function dot_product_d(a,ad,b,bd,ab)
	implicit none
	real, intent(in), dimension(:) ::  a,ad,b,bd
	real, intent(out) :: ab
	ab = dot_product(a,b)
	dot_product_d = dot_product(ad,b) + dot_product(a,bd)
end function dot_product_d

function transpose_d(v, vd, vt)
	implicit none
	real, dimension(:,:), intent(in) :: v, vd
	real, dimension(size(v,2), size(v,1) ) :: transpose_d
	real, dimension(size(v,2), size(v,1) ), intent(out) :: vt

	vt = transpose(v)
	transpose_d = transpose(vd)
end function transpose_d

    Notes:

    I have obtained strange results (automatically declared local variables of wrong size) from TAPENADE, when not used local variables for transposed variables. I don’t know the reason, but such behaviour of TAPENADE can avoided by some minor revisions to available code, as in the case of this example.

    Tags:, ,
    Posted in Fortran, Programming, TAPENADE | 13 Comments »